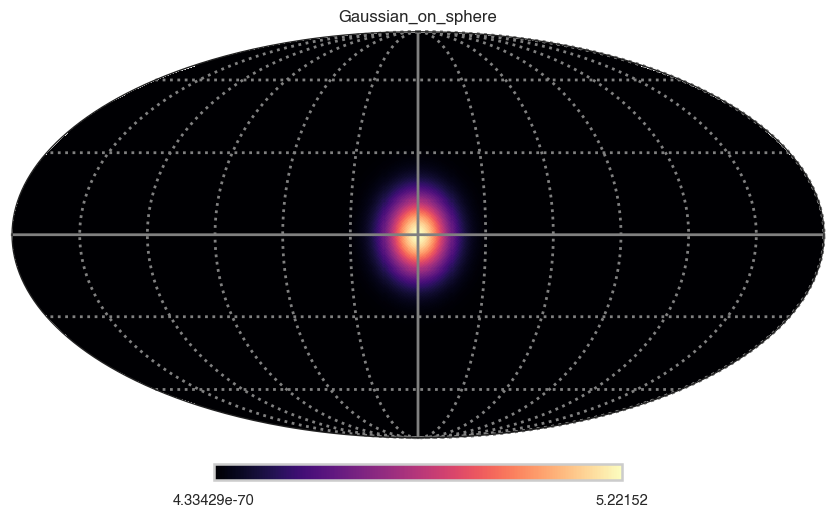
Gaussian on sphere

[3]:

# Parameters
func_name = "Gaussian_on_sphere"

Description

[5]:

func.display()

description: A bidimensional Gaussian function on a sphere (in spherical coordinates)
formula: $$ f(\vec{x}) = \left(\frac{180^\circ}{\pi}\right)^2 \frac{1}{2\pi \sqrt{\det{\Sigma}}} \, {\rm exp}\left( -\frac{1}{2} (\vec{x}-\vec{x}_0)^\intercal \cdot \Sigma^{-1}\cdot (\vec{x}-\vec{x}_0)\right) \\ \vec{x}_0 = ({\rm RA}_0,{\rm Dec}_0)\\ \Lambda = \left( \begin{array}{cc} \sigma^2 & 0 \\ 0 & \sigma^2 (1-e^2) \end{array}\right) \\ U = \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & cos \theta \end{array}\right) \\\Sigma = U\Lambda U^\intercal $$
parameters:
- lon0:
  - value: 0.0
  - desc: Longitude of the center of the source
  - min_value: 0.0
  - max_value: 360.0
  - unit:
  - is_normalization: False
  - delta: 0.1
  - free: True
- lat0:
  - value: 0.0
  - desc: Latitude of the center of the source
  - min_value: -90.0
  - max_value: 90.0
  - unit:
  - is_normalization: False
  - delta: 0.1
  - free: True
- sigma:
  - value: 10.0
  - desc: Standard deviation of the Gaussian distribution
  - min_value: 0.0
  - max_value: 20.0
  - unit:
  - is_normalization: False
  - delta: 1.0
  - free: True

The shape of the function on the sky.

[6]:

m=func(ra, dec)
hp.mollview(m, title=func_name, cmap="magma")
hp.graticule(color="grey", lw=2)